Pi in the Sky

In celebration of Pi day, I thought I'd post some quick and dirty PowerShell code you can use to calculate pi. I found some easy to follow explanations at http://www.wikihow.com/Calculate-Pi that weren't too difficult to transform into PowerShell code. And you might even learn something new about PowerShell along the way.

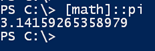
Before we begin, I hope you know that you can always get the value using the [Math] class:

But where's the fun in that? First up is my PowerShell version of Gregory-Leibniz series. This works by deriving pi from an infinite series.

π = (4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15)…

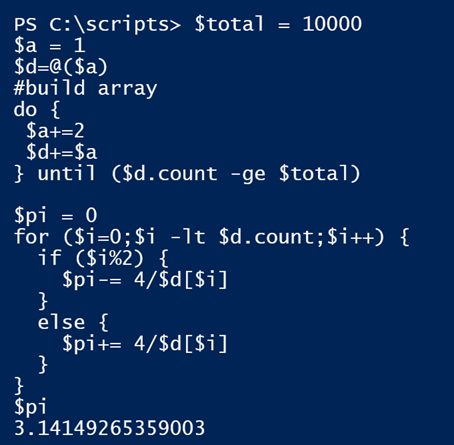
Seems simple enough. I need a large range of odd-numbered denominators. Then I need to alternately add and subtract. I'm going to need a loop and I can use the modulo operator (%) to test each time through the loop. If I am on an even number I'll add, otherwise I subtract. Here's what I came up with.

#total number of denominators to use
$total = 10000
$a = 1
$d=@($a)
#build array of odd numbers
do {
$a+=2
$d+=$a
} until ($d.count -ge $total)

$pi = 0
for ($i=0;$i -lt $d.count;$i++) {
if ($i%2) {
$pi-= 4/$d[$i]
}
else {
$pi+= 4/$d[$i]
}
}
$pi

This takes a little bit of time but it works.

Then I thought I'd try the Nilakantha series.

π = 3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - 4/(12*13*14) ...

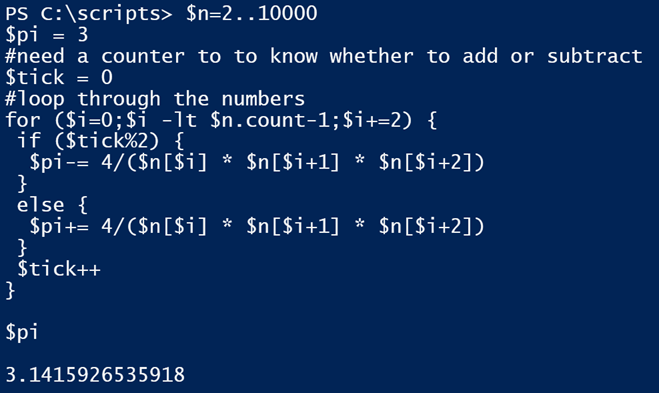
Some of the principals are the same. The tricky part here is looping through the collection of numbers and grouping them.

$n=2..10000
$pi = 3
#need a counter to to know whether to add or subtract
$tick = 0
#loop through the numbers
for ($i=0;$i -lt $n.count-1;$i+=2) {
if ($tick%2) {
$pi-= 4/($n[$i] * $n[$i+1] * $n[$i+2])
}
else {
$pi+= 4/($n[$i] * $n[$i+1] * $n[$i+2])
}
$tick++
}
$pi

This is noticeably faster and more accurate, well as far as you can be calculating an irrational number.

And the last way is using an Arcsine Function/Inverse Sine Function:

pi = 2 * (Arcsin(sqrt(1 - x^2))) + abs(Arcsin(x))

This gets a little tricky in PowerShell but it can be accomplished with the [Math] class. You have to watch out for the parentheses.

$x = 0.987654
$pi = 2 * (([math]::Asin([math]::Sqrt(1-([math]::Pow($x,2))))) + [math]::Abs([math]::Asin($x)))

The value of $x is between -1 and 1.

Also pretty quick, albeit a bit harder on the eyes to read.

Now if you'll excuse me I have some circles that need to be measured.

---

---